

Aβ aggregation leads to the formation of senile plaques. The number of new cases is growing daily due to a lack of reliable biomarkers for diagnosis and efficient treatments. Our results provide new insights on the role of CSF1R in microglia and how it interacts with the TREM2/β-Catenin and IL-34 system to clear Aβ and ameliorates the physiopathology of AD.Īlzheimer’s disease (AD) is a progressive neurodegenerative disorder and the most common form of dementia in the world.
Such a compensatory mechanism may promote microglial survival and phagocytosis of Aβ in the brain.

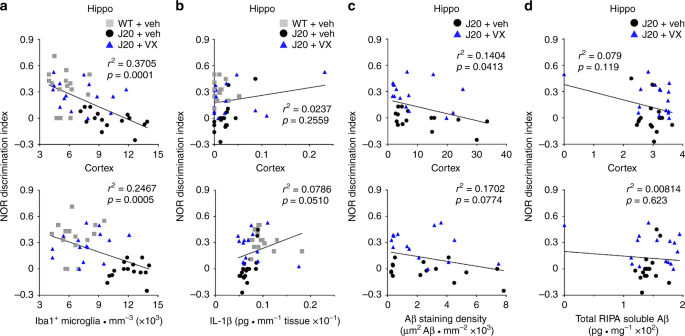
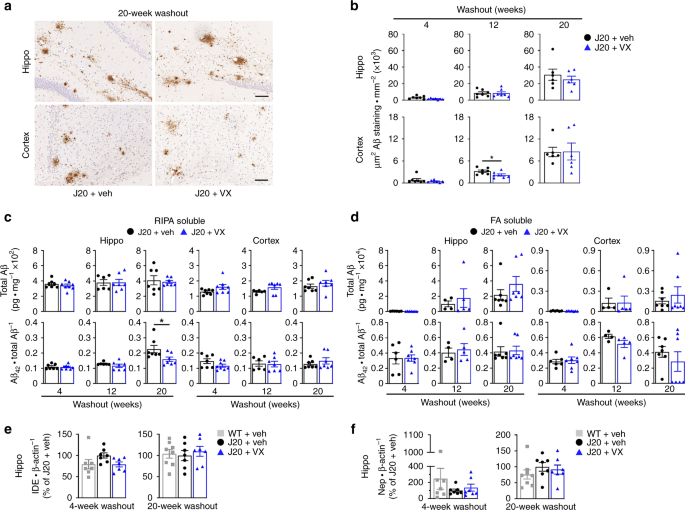
A compensating system seems to take place following the knockout, since TREM2/β-Catenin and IL-34 expression are significantly increased. Ameliorations of AD etiology are associated with a decrease in plaque volume in the cortex and hippocampus area. We have also shown that cognitive decline is delayed in CSF1R-deleted mice. Our findings demonstrated that CSF1R KO did not impair microglial survival and proliferation at 6 and 8 months of age in APP cKO compared to their littermate-control groups APP Swe/PS1. We induced the knockout at 3 months old, before plaque formation, and evaluated both 6- and 8-month-old groups of mice. We deleted CSF1R using Cre/Lox system the knockout (KO) is restricted to microglia in the APP/PS1 mouse model. Here, we investigate the impact of such receptor on AD etiology and microglia. Microglia are the innate immune cells of CNS their proliferation, activation, and survival in pathologic and healthy brain have previously been shown to be highly dependent on CSF1R. The corresponding numerical density of this bivariate size-number distribution can be stereologically determined from the estimated numerical density of the bivariate size-number distribution of the intersection profiles.Alzheimer’s disease (AD) is a progressive neurodegenerative disorder and the most common form of dementia in the world. Then the distribution of a spatially distributed ensemble of polyhedrons is determined by its size-number distribution. the number of vertices) are random variables. It is assumed that the size of the polyhedrons and the number of points (i.e. Secondly, random polyhedrons are constructed as the convex hull of points which are uniformly distributed on surfaces of spheres. The size-shape distribution of a stationary and isotropic spatial ensemble of regular prisms can be estimated from the size-shape distribution of the polygons observed in a section plane. First, regular prisms are considered which are described by their size and shape. Two models of random polyhedrons are investigated. We suggested computing the kernel function of the respective stereological integral equation by means of computer simulation. A general method for solving stereological problems for particle systems is applied to polyhedron structures.


 0 kommentar(er)
0 kommentar(er)
